Summary
In this lesson students will explore diatonic thirds and sixths
Age:
7-13 years
Lesson duration:
60 minutes
- Introduction: Ask students to draw a circle with seven points and label each point with numbers 1-7. (5 min)
- Have students find the distance from point “1” to point “3”. This is a third. Have students also find the distance from point “1” to point “6”. This is a sixth. (5 min)
- Have students use their circle to also find other ways of arriving at thirds. For example, from “2” to “4” is a third. (5 min)
- Have students use their circle to also find other ways of arriving at sixths. For example, from “3” to “1” (above) is a sixth. (5 min)
- Introduce students to the “scalar interval” block. A “third” is represented by the number “2” (two points above). A “sixth” is represented by the number “5” (five points above). Have students use this block on different starting pitches and listen to the results. (10 min)
- Have students use the Phrase Maker to create a simple melody. Then have students use thirds on the generated Action block and listen to the results. (10 min)
- Have students use the Phrase Maker to create a different simple melody. Then have students use sixths on the generated Action block and listen to the results. (10 min)
- Have students configure their generated Action blocks with Scalar Interval (set to thirds and sixths) in some sort of musical form (e.g. AABA). Have students share their creations. (10 min)
Number of Students
Up to 10.
Rationale
In music, thirds and sixths are very common. However, without explicit instruction students often do not recognize where they occur (even in music they may already be performing well). This lesson will introduce thirds and sixths to help young musicians to recognize them when they hear and read them.
Objectives
This lesson seeks to help students better recognize diatonic thirds and sixths.
Lesson
Introduction
Ask students to draw a circle and place seven points, evenly spaced. Each point should get a number 1-7.
For teachers working online, or who otherwise want to use Music Blocks as their whiteboard, you can use the following snippet of code.
[[0,["start",{"id":1600452186572,"collapsed":false,"xcor":214.00000000000045,"ycor":-274,"heading":90.0000000000001,"color":40,"shade":80,"pensize":5,"grey":157.14285714285714}],366,208,[null,32,null]],[1,"arc",1296,655,[11,4,3,null]],[2,["number",{"value":360}],1456,655,[4]],[3,["number",{"value":100}],1370,718,[1]],[4,"divide",1370,655,[1,2,5]],[5,["number",{"value":7}],1456,687,[4]],[6,["storein2",{"value":"box1"}],1282,336,[21,7,13]],[7,["number",{"value":1}],1388,336,[6]],[8,"show",1296,496,[23,9,10,25]],[9,["number",{"value":24}],1370,496,[8]],[10,["namedbox",{"value":"box1"}],1370,528,[8]],[11,"incrementOne",1296,623,[16,12,1]],[12,["namedbox",{"value":"box1"}],1379,623,[11]],[13,"repeat",1282,368,[6,14,17,null]],[14,["number",{"value":7}],1384,368,[13]],[15,["heading",{"value":38.57142857142867}],1402,400,[17]],[16,"setheading",1296,591,[25,18,11]],[17,["storein2",{"value":"box2"}],1296,400,[13,15,19]],[18,["namedbox",{"value":"box2"}],1402,591,[16]],[19,"setheading",1296,432,[17,20,23]],[20,["number",{"value":0}],1402,432,[19]],[21,"setcolor",1282,304,[27,22,6]],[22,["number",{"value":40}],1367,304,[21]],[23,"setcolor",1296,464,[19,24,8]],[24,["number",{"value":80}],1381,464,[23]],[25,"setcolor",1296,559,[8,26,16]],[26,["number",{"value":40}],1381,559,[25]],[27,"setheading",1282,272,[31,28,21]],[28,["number",{"value":90}],1388,272,[27]],[29,["action",{"collapsed":false}],1268,231,[null,30,31,null]],[30,["text",{"value":"7 Point Circle"}],1400,240,[29]],[31,"hidden",1282,272,[29,27]],[32,["nameddo",{"value":"7 Point Circle"}],380,249,[0,null]]]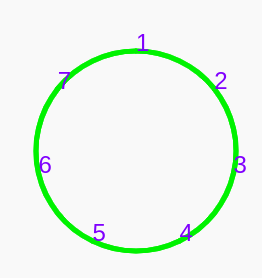
Part 1
A. Exploring thirds on paper (simple)
- Ask students to find points “1” and “3”. This is the distance of a third.
- Ask students to also find points “1” and “6”. This is the distance of a sixth.
The following questions are recommended to help reinforce for the student 3rds and 6ths. I have found these simple questions to be sufficiently challenging to many students.
- How many points up did I move to get from “1” to “3”? (Answer is “2”)
- (Question above rephrased:) Imagine we are playing a board game. If I were rolling a die, what number would I need to roll to get from “1” to “3”?
- How many points up did I move to get from “1” to “6”? (Answer is “5”)
- (Question above rephrased:) Imagine we are playing a board game. If I were rolling a die, what number would I need to roll to get from “1” to “6”?
- What number would “1” be if we kept going after “7”, wrapping around?
B. Exploring thirds on paper (more advanced)
Often, I find that student have trouble recognizing thirds and sixths because the reference pitch is always changing. In this section, you will ask students to find the third/sixth above numbers other than “1” in order to help their ability to recognize thirds/sixths from various reference points.
The following are recommended possibilities (easy):
- Find the third above “2”
- Find the third above “3”
- Find the third above “4”
- Find the sixth above “2”
The following are recommended possibilities (challenging):
- Find the third below “3”
- Find the third below “2” (wraps around)
- Find the sixth above “3” (wraps around)
- Find the sixth above “4” (wraps around)
At this point it would be helpful to point out to students that numbers 1-7 can represent pitches in a scale. Sing or play for students a diatonic scale while you sing or say the numbers (of the scale degrees). Then you might sing some thirds (e.g. Sing scale degrees 1, 2, 3, then 1 and 3).
C. Introduce Scalar Interval Block
Music Blocks has a Scalar Interval block, which is used to make simultaneously sounding pitches such as thirds and sixths.
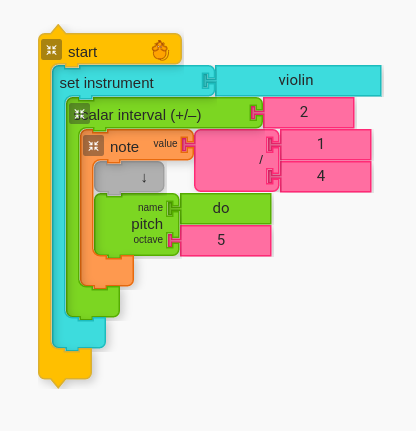
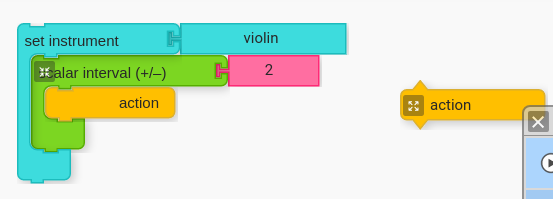
The following is an example of a third, starting from Do (scale degree 1 for C major by default). Have students create the following configuration.
Important: Note that Scalar Interval expects the number value for how many steps up or down to arrive at the interval. Therefore, a third is “2” (i.e. one moves up or down two diatonic pitches in the scale to arrive at the third). This is analogous to the board game question suggested above.
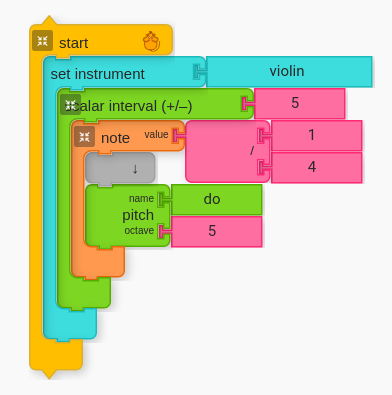
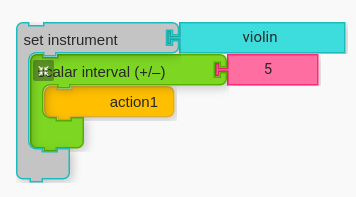
Next, have students create a diatonic sixth. Ask students what number they will need to put in for Scalar Interval to arrive at a sixth. (The answer is “5”)
Ask students to try Scalar Interval set to 2 (third) and Scalar Interval set to 5 (sixth) on different starting pitches (i.e. pitches other than Do).
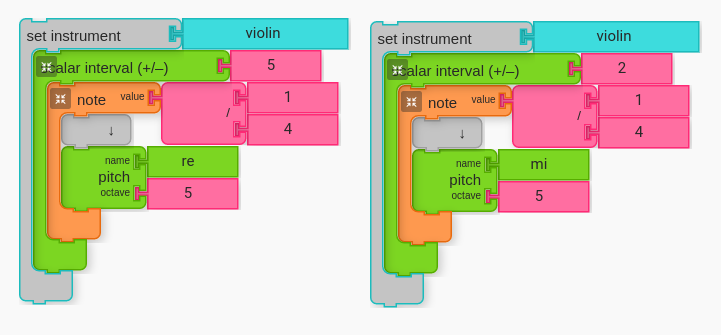
At this point, you might ask students to also figure out the scale degrees (1-7) for the starting pitch (inside the Note Value clamp) as well as the interval pitch (produced by Scalar Interval block).
D. Phrase Maker to Create Melodies
Ask students to use Phrase Maker to create melodies that they will use for their their thirds and sixths.
Students will need to pull a new Phrase Maker and create a melody that they like (it must have pitches).
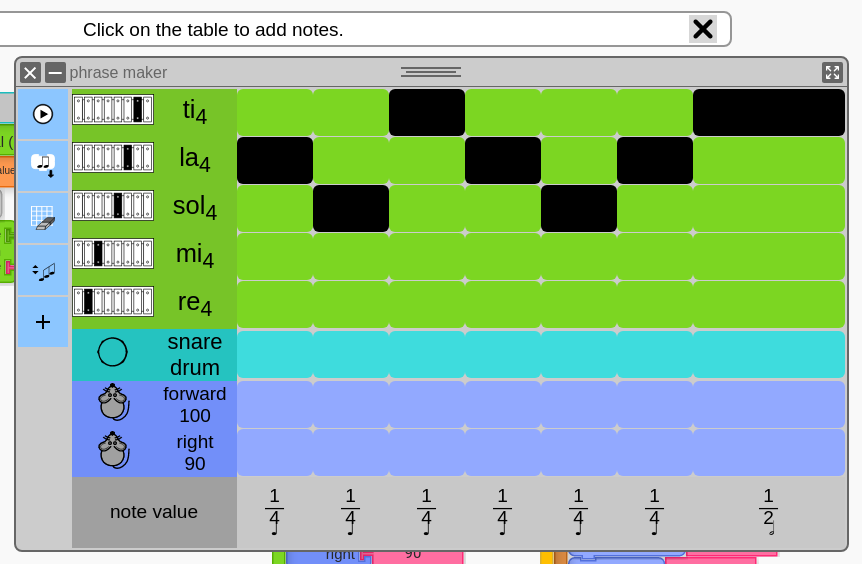
Students need to export their creation as Action blocks.
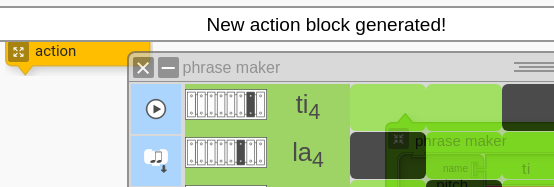
Ask students to use their Scalar Interval block that is set to “2” (a third) and clamp around their new Action block (from inside the action palette).
Have students repeat the process to create a new melody to be performed in sixths.
Any melodies are okay, but challenge students to find something that they really like.
G. Put it all together!
Ask students to give their Action blocks meaningful names. “A” and “B” are good names, and so are descriptive names (e.g. “funny”, “serene”, “whacky melody”, “Beethoven Remix”, etc.). Then have students order their phrases to create some sort of musical form.
The following has the same form as Hot Cross Buns (AABA):
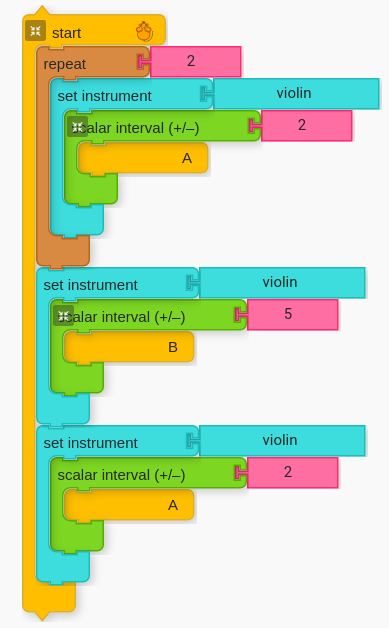
H. Extension: Comparison
Thirds and Sixths are pleasing, harmonious, consonant intervals. After completing the lesson, it is nice to try the harsh, dissonant intervals. You might ask students to try 2nds and 7ths, for example.
By this point, students will probably be able to figure out what number they need to input into Scalar Interval to get a 2nd or a 7th, so first ask them to see if they can figure it out. Once they know what numbers to put in (i.e. “1” for seconds and “6” for sevenths) have the students try those combinations and listen to the results.
The following is student work:
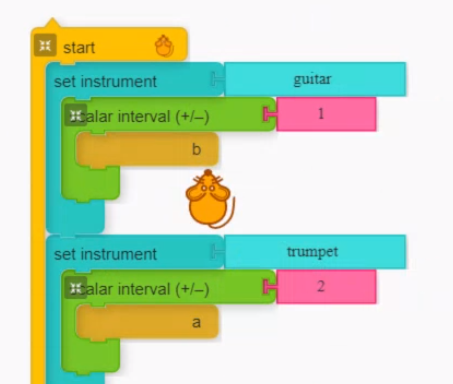
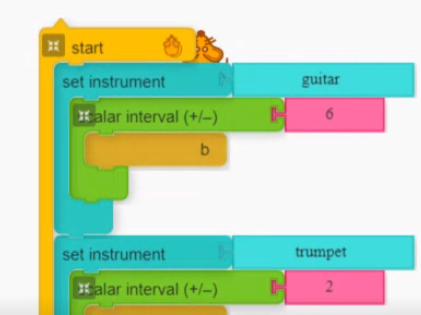
Ask students to describe, in their own words, how these intervals sound different from thirds and sixths.
Performance/Critique
- Have students showcase their creations for one another.
- Have students share anything new they noticed about thirds and sixths during the lesson.
Materials
- Paper and pencils for each student
- Music Blocks software (Computer, up-to-date browser)
Assessments
- Observe participation
- Do the students understand the concept of placement (third, sixth) from a reference point (1st point, 1st scale degree)?
- Do the students’ creations utilize thirds and sixths?
- Are the students able to recognize thirds and sixths from different reference points?
- Are students hearing the difference between thirds and sixths?
