Summary

In this lesson students will explore two different ways to create harmonics.

Music Blocks allows you to create harmonics by hand, using arithmetic tools, as well as via a “harmonic” blocks.

This lesson is similar to “Exploring the Harmonic Series”, but more basic.

Age:

7-13 years

Lesson duration:

60 minutes

  • As a group, try harmonics on an instrument, such as a monochord of guitar. (10 min)
  • Introduce (or reintroduce) the Hertz block. (10 min)
  • Use arithmetic on Hertz blocks to create new pitches. (10 min)
  • Use box to step through the harmonic series. (10 min)
  • Introduce harmonic blocks and compare methods. (10 min)
  • Create a random pitch generator (for fun). (10 min)

Number of Students

Up to 10.

Rationale

Music Blocks has many different ways to express the same idea. For expressing harmonics, students can do the math using arithmetic (i.e. multiplication and box blocks), Hertz block, and Set Instrument block set to “sine”. Or they can use the harmonic block. I prefer to start students with the more challenging way first, and then introduce the easier way. For this lesson, doing the arithmetic is more challenging, whereas using the harmonic block is easier.

Objectives

To explore harmonics. Students will explore the sound of harmonics, the math behind harmonics, and little bit about how they can be used in music.

Lesson

Introduction

Show students harmonics. If you have a string instrument such as a guitar or ukulele, they are perfect instruments to demonstrate harmonics. If you do not have any instrument, you can demonstrate harmonics with your voice by starting with your mouth closed while humming and slowly opening your lips apart while listening to the harmonics escape incrementally.

It can also be fun to perform a melody that can be played entirely with harmonics. For example “Day is Done” (Taps) can be performed entirely with harmonics on a single string.

Part 1

A. Hertz Block

Introduce (or reintroduce) students to the Hertz block.

A good starting point is with a pitch of A (or La). Musicians often tune their instruments to A 440, which is pitch A at 440Hz. Since 440 is a relatively simple whole number, and other pitches are not so simple, it is a good place to start.

As we will explore in this lesson as well as others, halving the Hz will bring you to the octave below and doubling the Hz will bring you to the octave above. Therefore, 220Hz is equivalent to pitch La of octave 3 (see image below). This pitch A, by the way, is the same as the A string of a standard guitar.

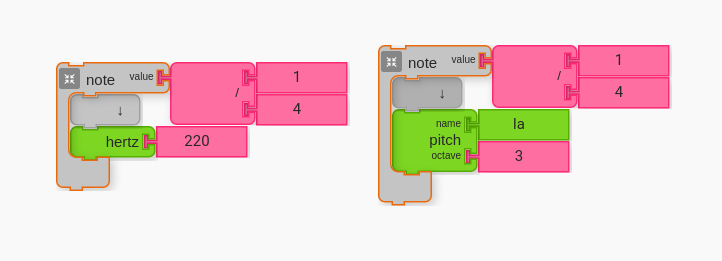
Hertz Block and its Solfege Equivalent
Hertz Block and its Solfege Equivalent

B. Arithmetic and Hertz Blocks


The next step is to prepare your code for arithmetic calculations.

Multiplying by one may seem like an unnecessarily obvious thing to do, but it prepares your code with the structure it needs to run various mathematical operations.

Have students add a multiplication and number block to formulate Hz = 220 * 1.

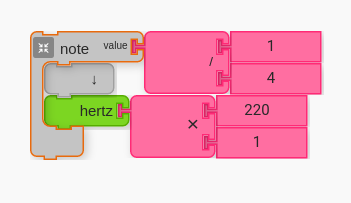
220Hz multiplied by 1. This structure is ready for math operations.
220Hz multiplied by 1. This structure is ready for math operations.

Have students try different multiples of 220Hz, such as multiplying by 2, 3, 4, 5 etc.

C. Increment in Multiples using Box

Next, create a simple algorithm using box to increment through different numbers to multiply by 220Hz. This should sound very similar to the harmonics (you can try playing through the harmonics on a standard guitar for comparison.

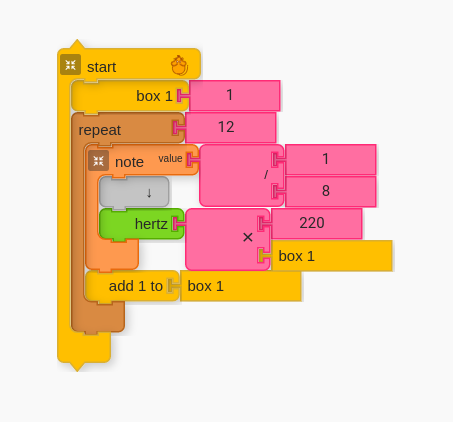
Use box to increment through multiples of Hz in the same way as harmonics.
Use box to increment through multiples of Hz in the same way as harmonics.

NOTE: For the script to sound more like a harmonic, use a Set Instrument block and set to “Sine”. Harmonics are simple sine waves.

D. Introduce Harmonic Block and Compare

Once students begin to solve the problem, task them to describing their method. How did they arrive at their solution? What was their strategy?

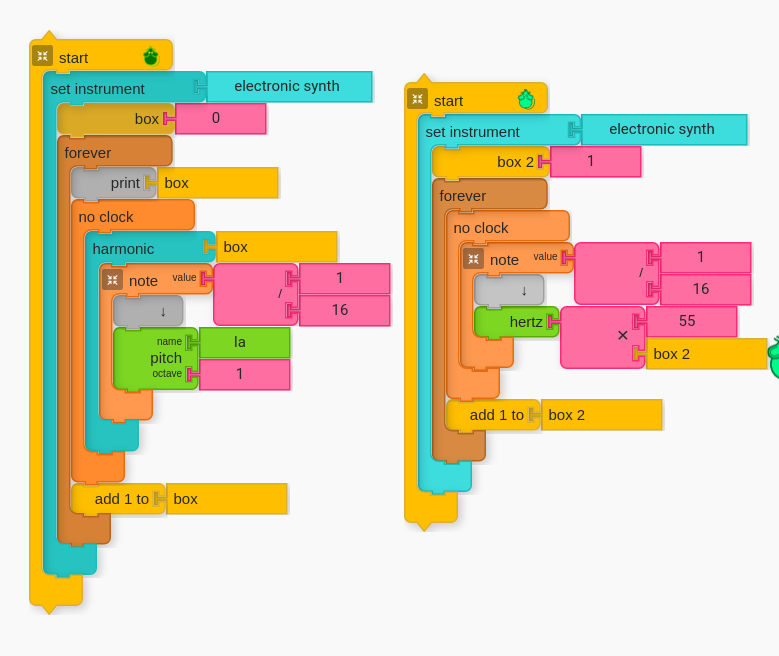
Introduce Harmonics Block and Compare
Introduce Harmonics Block and Compare | The script to the left uses harmonic block to step through the harmonic series. The script to the right uses arithmetic to step through the harmonic series. Notice that the Box block for each script has a different name (i.e. “box” vs. “box2”). NOTE: For the script to the right to sound more like a harmonic, Set Instrument block should be set to “Sine”.

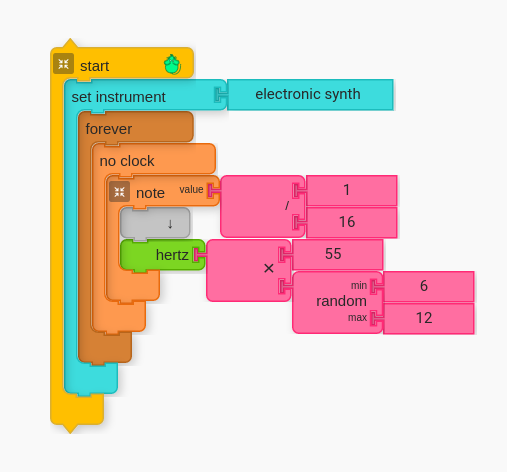
D. For Fun: Mix it Up!

Finally, have students play around with their code. One thing that I find fun is to create a “random pitch generator” by introducing the random block to the equation, resulting in unexpected (and sometimes “other-worldly”) melodies.

Random Pitch Generator (for Fun)
Random Pitch Generator (for Fun)

Performance/Critique

  1. Ask students what they learned about harmonics during the lesson.
  2. Ask students what they wonder about harmonics now that they have done the lesson.
  3. Have students create their own versions of the projects (either in class or at home) and show their new versions. What is unique? Does it explore something new with harmonics?

Materials

  • Music Blocks software (Computer, up-to-date browser)
  • If possible, a guitar or other stringed instrument.

Assessments

  • Observe participation
  • How do the students use arithmetic to create harmonics?
  • Do students make the connection between the two ways of creating harmonics with Music Blocks?
  • What remixing choices did students make?