Background

Musician Rob Flax is the one to first introduce me to the Collatz Conjecture during one of our collaborative concerts for the Music-in-Education department at New England Conservatory. We all created music around a math and music theme. His piece used the Collatz Conjecture as a framework for its musical form. (His piece was performed at one of our Music+Code events. Check it out at [Video to be published on remakemusic.net blog] )

Since the time of Rob introducing me to the conjecture, I have long wondered what the output would sound like as pitches. However, I had never had a good tool to test the idea. That is, until Music Blocks! …but even after Music Blocks became robust, I myself struggled to formulate my idea as logical code. I made some vain attempts that all ended in failure.

Recently, in the late summer of 2021, I was reading Lockhart’s Lament, an article urging for more sincere problem-solving in math for primary education. The article got me really excited on a number of different levels. In particular, it was exhilarating to think of the challenges of problem-solving a problem for which there is no known answer. This reminded me on the Collatz Conjecture. I tried to create a program once more, and this time I succeeded.

Summary

In this lesson students will explore the Collatz Conjecture with conditionals, music, and visualization. Students are challenged to problem solve as well as to make artistic choices.

Advanced students should be challenged to find their unique solution to the challenge. Beginners can be given a complete version of the program and asked to try different numbers (it’s like a game).

Age:

10-12 years

Lesson duration:

60 minutes with follow-ups for refinement

  • Introduction: Introduce the Collatz Conjecture. (10 min)
  • Work with students to create code that will mimic the Collatz Conjecture algorithm. (10 min)
  • Work with students to map out the structure. What features are needed? Where do we put the code? (15 min)
  • Together with students, design and implement artistic choices. (15 min)
  • Play the program for each other and critique. (10 min)
  • Return to student creations the next time you meet for improvements (as time allows)

Number of Students

Up to 10.

Rationale

Visualization is an important way to understand data trends, which can help you make predictions and make new hypotheses. Since Music Blocks has many art features, it is a great tool for creating visualizations.

By applying the principles of visualization to hearing, you get “auralization”. Data trends can be represented as audio and presented to be heard. Music Blocks’ many music features make auralization possible.

The lesson can be applied to many formulae and data sets. This lesson focuses on the Collatz Conjecture, which is based on a simple formula that uses basic arithmetic. The simple math helps to make this project doable for students. The Collatz Conjecture is also, as of now, unproven. This fact makes the lesson exciting (Who knows? Maybe a program that a student creates will help us get a step closer to proving or disproving the conjecture.) Lastly, for any unique input, the output path will always be the same. This means that it is not random, despite seeming random. The pseudo-predictability of the output helps learners catch flaws in their programs.

Objectives

Students will have more experience problem solving by creating their own visual and audio expression of the Collatz Conjecture.

Lesson

Introduction

Introduce the Collatz Conjecture. For more information on this famous problem, please read the Music Blocks blog article and Wikipedia article on the conjecture. The video on Collatz Conjecture created by Veritasium is also very informative.

After introducing the Collatz Conjecture, if time allows, engage students in a discussion.

Part 1

A. Expressing The Equation, The Algorithm

The equation for the Collatz Conjecture is quite simple.

  • Take as input any positive whole number.
  • If the number is even, divide it by two.
  • If the number is odd, multiply it by three and add one.
  • Repeat with the new output as input.

Together as a class, sketch this equation on the board. What features does it have (e.g. multiplication, division, repetition, conditional test, etc)?

Next, ask students to use their knowledge of Music Blocks to plan what the expression of this equation would be as code. What blocks are needed? How would they be configured? How do we test for odd and even?

The following image shows the solution that I came up with. Note how the input is determined to be odd or even by utilizing mod. (Tip: One way to think of mod is as the “remainder”. In the case of mod(2), what is the remainder of a given number when dividing by two.)

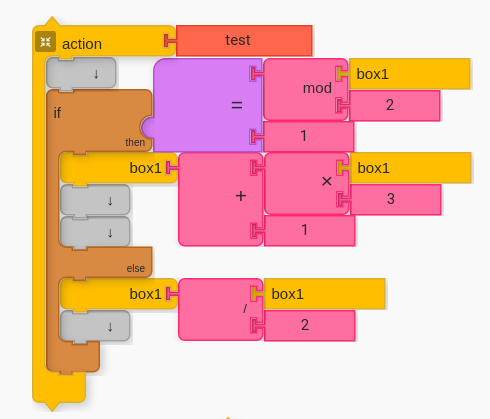
If odd, multiply by 3 and add 1. If even, divide by 2.

Let the Learners Struggle!

Going back to my inspiration for this lesson as described in Background, the part of this problem I personally struggled with was how to test odd and even. In fact, creating this program I realized how much we take for granted the idea of odd and even. It is so simple for an educated human to just look at a number and say, “that’s odd” or “that’s even”, but it is far trickier to program a computer, with a limited but complete set of utilities to say, “this is my elegant, efficient computational test for odd and even”.

I expect students will struggle with this as well. But, as also hinted at in the background, the struggle is a large part of the point of learning. As best as you can, I encourage you to allow students to struggle with this problem (or another unique problem), to come up with a solution.

My solution was to use modular arithmetic for a space of two. This way, any number divisible by two would output as zero, and any other (odd) number would output as one. This kept the test fairly simple. This is a fairly mathematical approach to the solution. Other solutions could involve moving the Mr. Mouse glyph around the screen and testing its position, or using a change in pitch and testing the resulting scale degree (both of which, as of this writing, are unexplored as to my knowledge, but likely to work.

B. Create the Code

Next, work with students to create a functional structure for their program.

Discuss with students the different features the entire program will need to have both visual and audio output. What structure is needed for the output to remain faithful to the input, without unnecessary or misleading distortions?

Some of the necessary features will likely be:

  • Number Input
  • Odd-Even Test (created in previous section)
  • Method for testing whether or not we are in the final 4 – 2 – 1 loop (not yet shown in image below)
  • Method for testing whether the input number is a positive whole number (the image below tests for positivity, but not for whole number status)
  • Audio and Visual Output
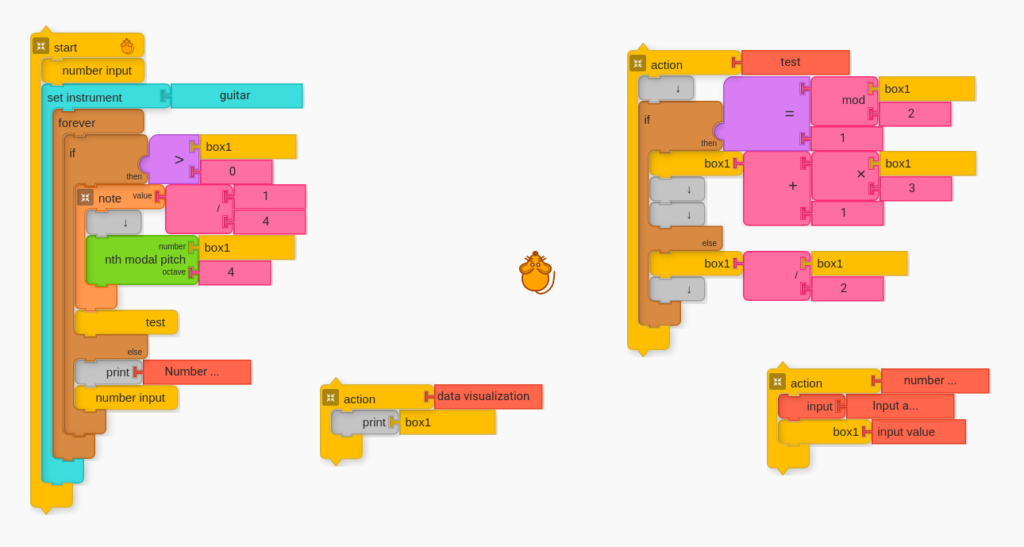
An example of functional code without embellishments.

A Note about Process — Big Picture and Small Picture

Teachers can help facilitate the design process on the board. The design does not need to be perfect, but the teacher should challenge students to consider the various challenges. Once students have began implementing the design within Music Blocks, they will inevitably have more questions. One approach that I recommend is asking students to put Action blocks in as placeholders, even before the details are in place. For example, in the above image, the “data visualization” Action block only prints the number in box1. This can be fleshed out later, and it can be helpful to keep things bare while working on the big picture.

Students frequently get stuck working on a subset of the larger problem. When this happens, encourage students to focus on other aspects of their code and come back to the smaller details later.

C. Creative Choices for Audio and Visual Output

Once students have a functional framework, they should be encouraged to add the audio and visual output.

Students have a lot of latitude in this section. For example, do they want to try scalar or chromatic? Or maybe even Hertz? Do they want a rhythmic component? What colors do they want to display and how? How should the Mr. Mouse glyph move around the screen? How should screen space be used?

Work with students to make their own decisions, and nudge them if they have a difficult time deciding. It is important that they try and test their ideas (not just consider them).

D. Hailstorm Music: Putting it All Together!

Students should finish class with a functional creation. This is the fun part. Have students test their programs, and make some initial changes.

Because the output follows a kind of “hailstorm” pattern where output seems random, but trends downward, the musical and visual output is somewhat spontaneous. This makes the experience unpredictable and fun.

Here are some examples of complete projects (created by teachers):

[fvplayer id=”29″]
Output for 71 for Collatz Conjecture
Output for 71 for Collatz Conjecture

Have a remix to share? Please share it in the comments for https://musicblocks.net/2021/09/13/collatz-conjecture-math-data-visualization-and-music-blocks/

E. Extensions

This lesson can be very lightly explored with young beginners by asking them to just try complete projects. I have had students try the completed projects and have a lot of fun, trying numbers and marveling at the results. In fact, a few of my 2nd grade students from MAP Afterschool learned a bit more about odd and even from even this simple exposure.

Advanced students should be encouraged to figure out solutions (i.e. determining odd from even) themselves. This, of course, may cause the lesson to run over the planned 60 minutes. If time allows, then you should come back to this lesson again. In fact, there are many different things you can do with this initial project (as shown from the remixes above). Students can be challenged to come up with new visualizations and auralizations on their own.

Performance/Critique

  1. Have students perform their creation(s) for the group
  2. Engage in a discussion. What were the biggest challenges? What sort of things did you learn? What process did you use? What worked best? What could have been improved?

Materials

  • Music Blocks software (Computer, up-to-date browser)
  • Whiteboard or chalkboard for sketching out designs

Assessments

  • Observe participation
  • Do the projects calculate the Collatz Conjecture algorithm?
  • What process did students go by in implementing their designs?
  • What creating choices did students make?
  • What ideas are left unfinished? Do students have ideas for how to create them?