Lesson Plan: Interval Sudoku

Summary

In this lesson students will explore different types of contrapuntal motion via the n^th modal pitch block

Age:

7-13 years

Lesson duration:

60 minutes

• Introduction: Ask the group “What do you think when you think of the word interval?” “What about with music? What is a musical interval?” (10 min)
• Introduce n^th modal pitch by itself. Have students explore inputting different numbers. (10 min or skip if kids have used n^th modal pitch before)
• Have students open the pre-made “interval sudoku” project. Demonstrate the simpler types of motion (i.e. parallel, contrary, oblique) given two interactive pitches. (10 min)
• Have students try these motions on their own. (5 min)
• Demonstrate more complex patterning of the simpler types (e.g. 5-6 sequence to break up ascending parallel fifths). (10 min)
• Have students remix the demo version and/or find patterns and sequences that interest them.

Number of Students

Up to 10.

Rationale

The introduction of an additional pitch adds new possibilities to the sound. The pitches interact in ways called counterpoint. One pitch can stay still while the other moves, the two pitches can move in the same direction, or they can move in opposite directions. This may seem simple, but it is the starting point for an explosion of possibilities in the sound.

Objectives

The goal is to give students a few important compositional tools (and judgement) that they will inevitably need to consider when creating music. Also, the vocabulary of terms should be a goal of the class as the terminology will help students express themselves as well as make musical decisions.

Lesson

Introduction

Review: It is important, if it has not been done so already, that students understand how n^th modal pitch block works. This way of expression is probably unfamiliar to musicians, but it allows us to express pitch as a number, and with an index of zero, which allows for a limitless ability to traverse the pitches any mode.

Help students identify 0 as C (the first scale degree), 1 as D, and -1 as B (octave before) in C major. Ask students to guess what the other numbers will result in.

Interval: Ask the group about intervals “What do you think when you think of the word interval?” “What about with music? What is a musical interval?”

Part 1

A. Possibilities with two points

With two n^th modal pitch blocks the user can control two points. One way to make this interactive is by tying cursor x and y in the following manner:

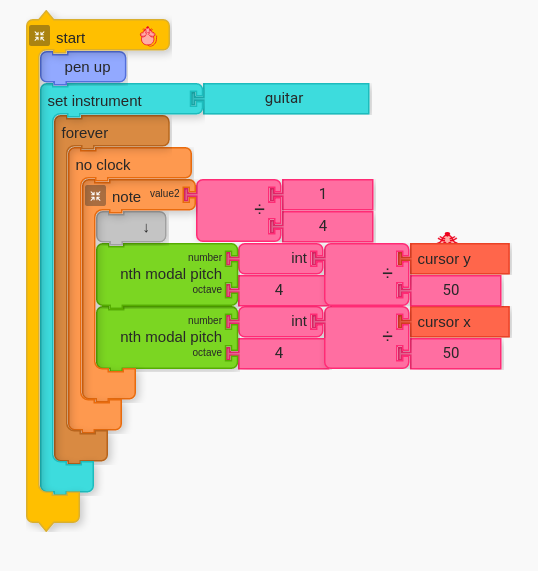
Below is the Music Blocks code for the above (you can copy and paste into MB with ctl-v):

[[0,["start",{"collapsed":false,"xcor":0,"ycor":0,"heading":0,"color":0,"shade":50,"pensize":5,"grey":100}],219,140,[null,25,null]],[1,"settimbre",233,213,[25,2,24,3]],[2,["voicename",{"value":"guitar"}],384,213,[1]],[3,"hidden",233,623,[1,null]],[4,"drift",261,277,[24,6,5]],[5,"hidden",261,561,[4,null]],[6,["newnote",{"collapsed":false}],275,309,[4,7,10,13]],[7,"divide",377,309,[6,8,9]],[8,["number",{"value":1}],463,309,[7]],[9,["number",{"value":4}],463,341,[7]],[10,"vspace",289,341,[6,11]],[11,"nthmodalpitch",289,373,[10,20,12,14]],[12,["number",{"value":4}],419,405,[11]],[13,"hidden",275,530,[6,null]],[14,"nthmodalpitch",289,436,[11,16,15,null]],[15,["number",{"value":4}],419,468,[14]],[16,"int",419,436,[14,18]],[17,["mousex",{"value":-347}],591,436,[18]],[18,"divide",505,436,[16,17,19]],[19,["number",{"value":50}],591,468,[18]],[20,"int",419,373,[11,21]],[21,"divide",505,373,[20,23,22]],[22,["number",{"value":50}],591,405,[21]],[23,["mousey",{"value":223.5}],591,373,[21]],[24,"forever",247,245,[1,4,null]],[25,"penup",233,181,[0,1]]]

The result will be a pulse of various intervals, but without a way to predict the sound before it plays. Asks students to open the grid.

After the students have experimented with the grid open for a minute or two, asks students to try just going up and down, then just left to right. Finally ask students to move diagonally. What do they hear? How can they describe what they hear?

B. Interval Sudoku

The simple example is a nice way to begin to see the simplest structure of the code, but it does not help us predict and experiment with different intervals in a useful way. Ask students to open the following project.

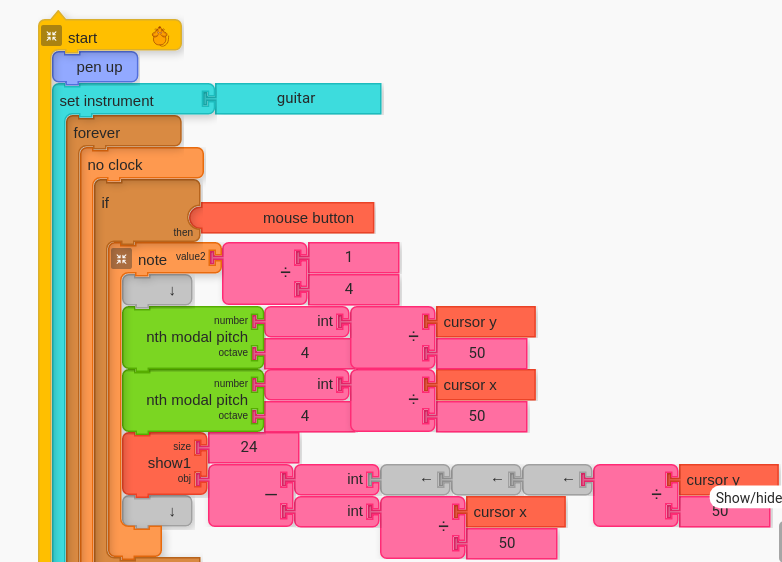
[[0,["start",{"collapsed":false,"xcor":-378,"ycor":317,"heading":0,"color":0,"shade":50,"pensize":5,"grey":100}],320,90,[null,45,null]],[1,"settimbre",334,163,[45,2,24,3]],[2,["voicename",{"value":"guitar"}],485,163,[1]],[3,"hidden",334,919,[1,null]],[4,"drift",362,227,[24,43,5]],[5,"hidden",362,857,[4,null]],[6,["newnote",{"collapsed":false}],390,322,[43,7,10,13]],[7,"divide",492,322,[6,8,9]],[8,["number",{"value":1}],578,322,[7]],[9,["number",{"value":4}],578,354,[7]],[10,"vspace",404,354,[6,11]],[11,"nthmodalpitch",404,386,[10,20,12,14]],[12,["number",{"value":4}],534,418,[11]],[13,"hidden",390,637,[6,null]],[14,"nthmodalpitch",404,449,[11,16,15,25]],[15,["number",{"value":4}],534,481,[14]],[16,"int",534,449,[14,18]],[17,["mousex",{"value":72}],706,449,[18]],[18,"divide",620,449,[16,17,19]],[19,["number",{"value":50}],706,481,[18]],[20,"int",534,386,[11,21]],[21,"divide",620,386,[20,23,22]],[22,["number",{"value":50}],706,418,[21]],[23,["mousey",{"value":264}],706,386,[21]],[24,"forever",348,195,[1,4,null]],[25,"show",404,512,[14,26,27,28]],[26,["number",{"value":24}],478,512,[25]],[27,"minus",478,544,[25,29,33]],[28,"vspace",404,575,[25,null]],[29,"int",564,544,[27,37]],[30,"divide",863,544,[39,31,32]],[31,["mousey",{"value":264}],949,544,[30]],[32,["number",{"value":50}],949,576,[30]],[33,"int",564,576,[27,34]],[34,"divide",650,576,[33,35,36]],[35,["mousex",{"value":72}],736,576,[34]],[36,["number",{"value":50}],736,608,[34]],[37,"hspace",650,544,[29,38]],[38,"hspace",721,544,[37,39]],[39,"hspace",792,544,[38,30]],[40,"setxy",390,669,[43,41,42,46]],[41,["mousex",{"value":-378}],464,669,[40]],[42,["mousey",{"value":317}],464,701,[40]],[43,"ifthenelse",376,259,[4,44,6,40,null]],[44,["mousebutton",{"value":false}],471,282,[43]],[45,"penup",334,131,[0,1]],[46,"print",390,732,[40,47,59]],[47,"minus",464,732,[46,48,55]],[48,"int",550,732,[47,49]],[49,"hspace",636,732,[48,50]],[50,"hspace",707,732,[49,51]],[51,"hspace",778,732,[50,52]],[52,"divide",849,732,[51,53,54]],[53,["mousey",{"value":316}],935,732,[52]],[54,["number",{"value":50}],935,764,[52]],[55,"int",550,764,[47,56]],[56,"divide",636,764,[55,57,58]],[57,["mousex",{"value":-378}],722,764,[56]],[58,["number",{"value":50}],722,796,[56]],[59,"vspace",390,764,[46,null]],[60,0,[0,"show",24,4]],[61,0,[0.6666666666666666,"show",24,5]],[62,0,[1.3333333333333333,"show",24,4]],[63,0,[2,"show",24,5]],[64,0,[2.6666666666666665,"show",24,4]],[65,0,[3.333333333333333,"show",24,5]],[66,0,[3.9999999999999996,"show",24,4]],[67,0,[4.666666666666666,"show",24,5]],[68,0,[5.333333333333333,"show",24,4]],[69,0,[6,"show",24,5]],[70,0,[6.666666666666667,"show",24,4]],[71,0,[7.333333333333334,"show",24,5]],[72,0,[8,"show",24,4]]]

Using the project above, have students try up-down, left-right, and diagonal motion again and observe the different numbers.

B. Oblique, Parallel, and Contrary

By having students move diagonally, they will always get parallel motion. The bottom example is parallel unison (both pitches are exactly the same).

The bottom example is also parallel motion. This is known in music as “parallel thirds” and is known for being a pleasant sound.

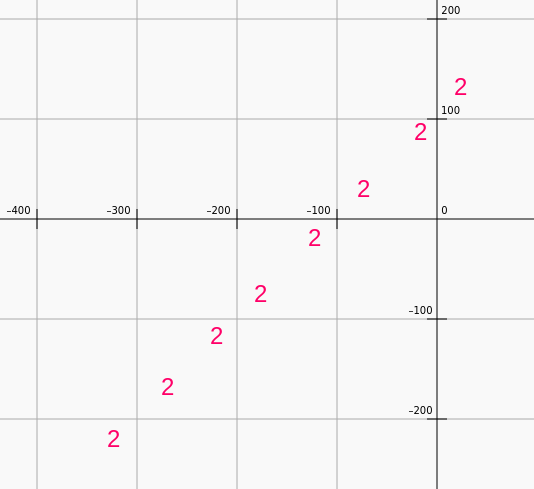
Moving up-down gives us oblique motion. One voice stays the same while the other moves.

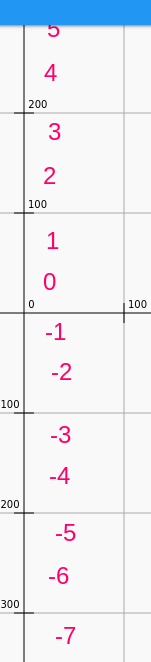
Moving left-right is another way to get oblique motion.

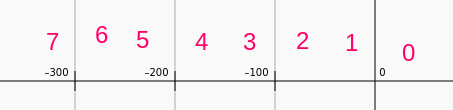
Finally, we have contrary motion. See below:

C. Change our Reference

By simply adding to just x or just y we can change our reference.

D. Mixing it up

Music only uses the aforementioned motion in brief succession. Typically, the motion is broken at some point. Here are some simple, yet common, ways to mix things up.

For example, let’s take fifths.

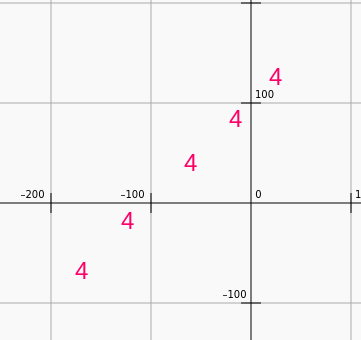
A very common way of moving up in pitch with parallel fifths is to break them up by going to the sixth in between. Going from left-bottom to right-top, have the students try the following.

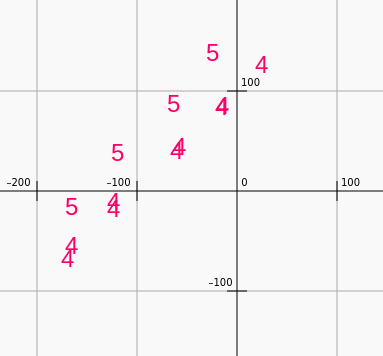
4-5-4-5-4-5 etc from left-bottom to right-top. How does the sound differ from plain parallel fifths?

Another way to mix things up is to try 2nd-3rd motion such as the following (from top-right to bottom left):

TODO: Replace image. Should have ones and twos.

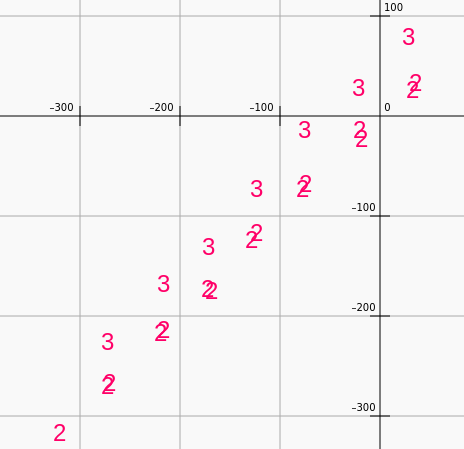
There are many other options such as the following.

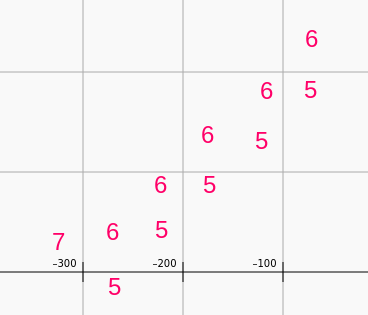
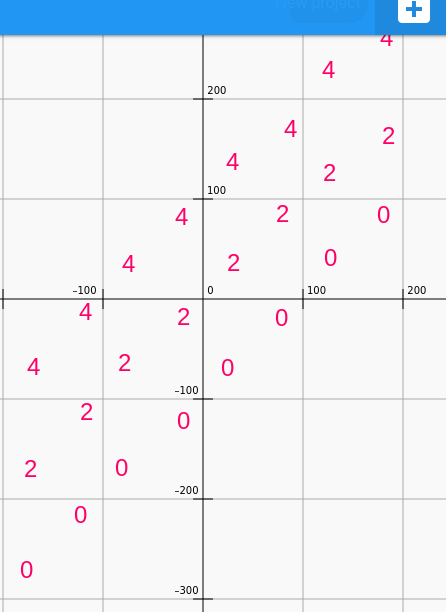
E. Arpeggios

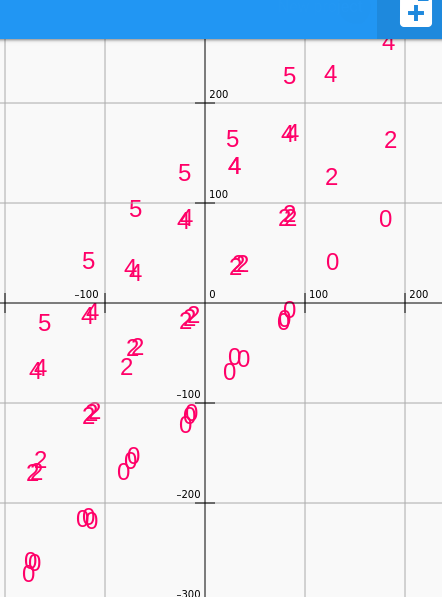
It is fun to skip notes and create arpeggios. The following outlines each chord as well as giving us a parallel motion and breaking parallel fifths by adding sixths.

And breaking up the parallels with the sixths (number 5)

Performance/Critique

1. Have students share some patterns that they like.
2. Have students comment on other’s combinations.

Materials

• Music Blocks software (Computer, up-to-date browser)
• Instruments, if possible

Assessments

• Observe participation
• Do the students pick up the terminology oblique, parallel, and contrary (or the general concept)?
• Are students able to hear the different types of motion?
• Are the students coming up with aesthetic decisions about what they like?