Lesson Plan: Dissonance to Consonance

Summary

This lesson builds upon the “thirds and sixths” lesson plan with motions into thirds and sixths (consonant intervals) from other (dissonant) intervals.

Age:

7-13 years

Lesson duration:

60 minutes

• Introduction: Discuss “tension” and “resolution”. How do stories use tension and resolution? (5 min)
• Review: Review 3rds and 6ths. (5 min)
• Motion into 3rds and 6ths: Use review material and ask how we can move to 3rds and 6ths from above and below. (5 min)
• Create a simple script to move from a 4th to a 3rd. (10 min)
• Create an action that moves us up the scale, while using the 4th to 3rd motion. (10 min)
• Modify the script to move from 2nd to 3rd instead. (5 min)
• Copy the scripts and create a way to preview all the possible ways to move to 3rds and 6ths from above and below. (10 min)
• Have students share their projects and discuss which combinations they like and why. (10 min)

Number of Students

Up to 10.

Rationale

In music, thirds and sixths are very common. However, without explicit instruction students often do not recognize where they occur (even in music they may already be performing well). This lesson will introduce thirds and sixths to help young musicians to recognize them when they hear and read them.

Objectives

This lesson seeks to help students hear dissonant to consonant motion.

Lesson

Introduction and Review

One way that I like to explain the motion from dissonance to consonance is this: Imagine a story. Stories typically have places of tension, which function very similarly to musical dissonance. When the tension is resolved, that functions very similarly to how a musical dissonance resolves to a consonance.

Ask students to come up with some ideas for a story. What would be something in the story that has tension, something that leaves the listener wondering what will happen next? Then ask students to think of how it would be resolved.

The focus for this lesson is the motion into 3rds and 6ths. Therefore, it would be helpful to review where 3rds and 6ths are on (single octave) pitch circle like the one below. Ask students what are all the ways we can approach the “3rd” and the “6th” by only moving up or down by one.

For teachers working online (screen sharing), or who otherwise want to use Music Blocks as their whiteboard, you can use the following snippet of code.

[[0,["start",{"id":1600452186572,"collapsed":false,"xcor":214.00000000000045,"ycor":-274,"heading":90.0000000000001,"color":40,"shade":80,"pensize":5,"grey":157.14285714285714}],366,208,[null,32,null]],[1,"arc",1296,655,[11,4,3,null]],[2,["number",{"value":360}],1456,655,[4]],[3,["number",{"value":100}],1370,718,[1]],[4,"divide",1370,655,[1,2,5]],[5,["number",{"value":7}],1456,687,[4]],[6,["storein2",{"value":"box1"}],1282,336,[21,7,13]],[7,["number",{"value":1}],1388,336,[6]],[8,"show",1296,496,[23,9,10,25]],[9,["number",{"value":24}],1370,496,[8]],[10,["namedbox",{"value":"box1"}],1370,528,[8]],[11,"incrementOne",1296,623,[16,12,1]],[12,["namedbox",{"value":"box1"}],1379,623,[11]],[13,"repeat",1282,368,[6,14,17,null]],[14,["number",{"value":7}],1384,368,[13]],[15,["heading",{"value":38.57142857142867}],1402,400,[17]],[16,"setheading",1296,591,[25,18,11]],[17,["storein2",{"value":"box2"}],1296,400,[13,15,19]],[18,["namedbox",{"value":"box2"}],1402,591,[16]],[19,"setheading",1296,432,[17,20,23]],[20,["number",{"value":0}],1402,432,[19]],[21,"setcolor",1282,304,[27,22,6]],[22,["number",{"value":40}],1367,304,[21]],[23,"setcolor",1296,464,[19,24,8]],[24,["number",{"value":80}],1381,464,[23]],[25,"setcolor",1296,559,[8,26,16]],[26,["number",{"value":40}],1381,559,[25]],[27,"setheading",1282,272,[31,28,21]],[28,["number",{"value":90}],1388,272,[27]],[29,["action",{"collapsed":false}],1268,231,[null,30,31,null]],[30,["text",{"value":"7 Point Circle"}],1400,240,[29]],[31,"hidden",1282,272,[29,27]],[32,["nameddo",{"value":"7 Point Circle"}],380,249,[0,null]]]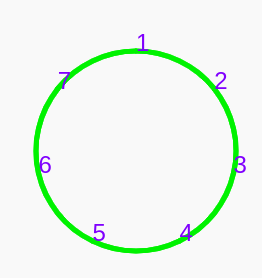

The above is something asked of the students from the previous lesson on thirds and sixths. You could have students circle “3” (for 3rd) and “6” (for 6th). These are our consonant intervals. Then ask how they can move to these places by only moving one. The starting places are the dissonant intervals, the places of tension.

Part 1

A. Exploring fourth to third

First start with some simple questions to review how we use Scalar Interval to get to a 4th and a 3rd.

1. Ask students to find a fourth above tonic. Ask, “How many up do we need to move to get to a forth?” (Answer: We need to go up “3”)
2. Ask students to find a third above tonic. Ask, “How many up do we need to move to get to a third?” (Answer: We need to go up “2”)

The following is the Music Blocks code for moving from a scalar 4th to a scalar 3rd. Ask students to create the following.

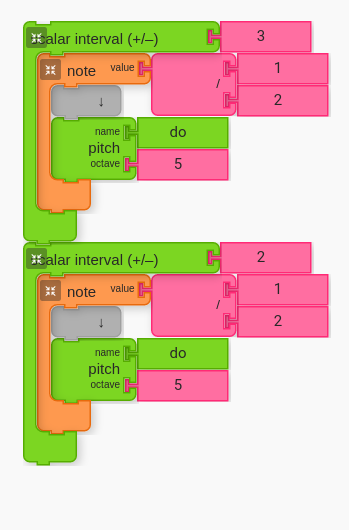
Notice that the affected pitch remains the same (i.e. both pitches are “do”). It is important that both pitches are the same otherwise the “resolution” will lose context with regard to the tension set up before it.

B. 4th-3rd Moving Up

The 4th to 3rd motion is nice, but it is better to move around the scale to “taste” the different possibilities. Below is an explicit spelling of 4th to 3rd starting from “Do” and then 4th to 3rd starting from “Re”.

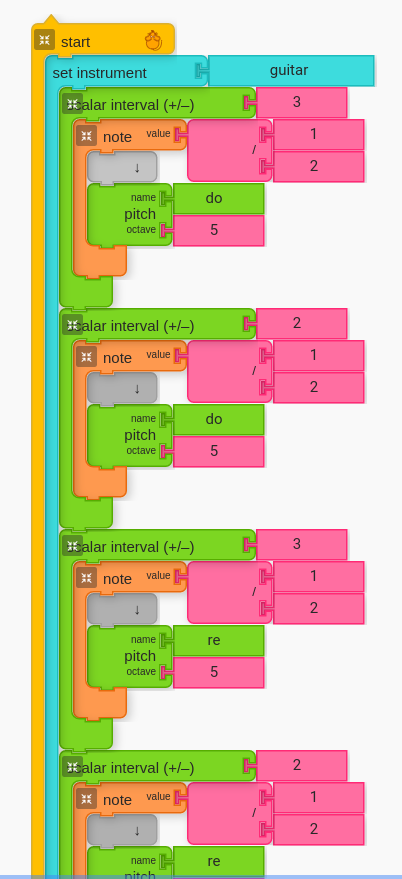
Like before, it is important that for the tension (4th) and resolution (3rd) to have the same reference pitch inside (before moving up).

C. Using Scalar Step to Automate Movement

Ask students if they can think of another way to move up that automates the process of moving up. One way is to use the “scalar step” block.

Students can try the following to step the next pitch up.

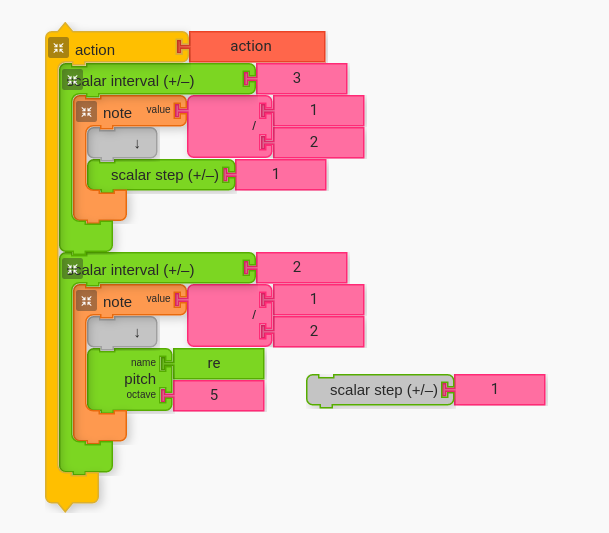
If the second note (i.e the one with the 3rd) were to also have a scalar step of +1 then the reference point for the intended resolution would change which ruins the resolution. Ask students to try and think of how they can keep the second pitch the same without moving it up (or down).

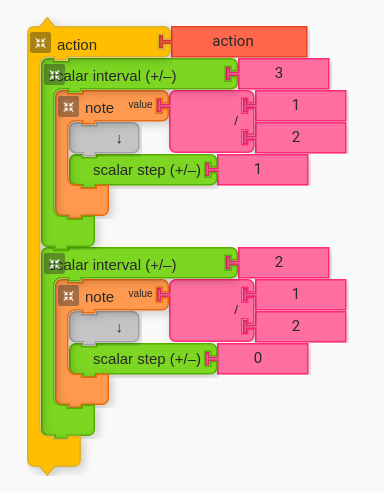
We can now use scalar step to move up automatically. The following has an action block (corresponding to the block spelled out above) that repeats 7 times. Because we use the scalar step block the first time, it will change its reference pitch every first iteration (when playing the fourth).

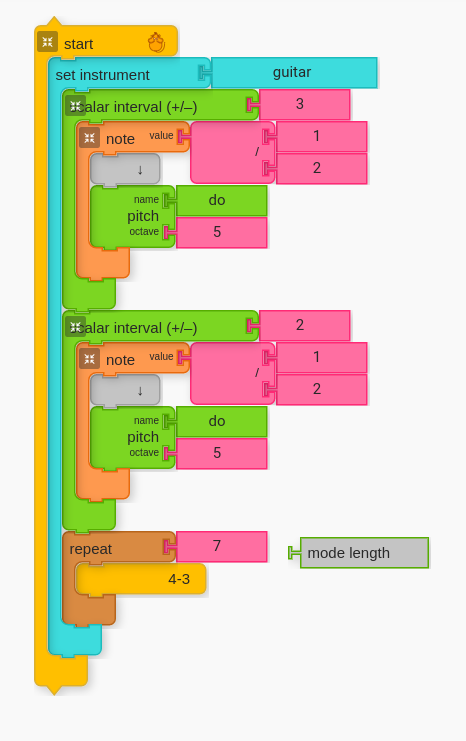
If we want to go up the entire scale to hear the 4th-3rd motion for all the possible notes in the scale, then we can use the “mode length” block. This will allow us to repeat as many pitches as their are in the scale (regardless the scale).

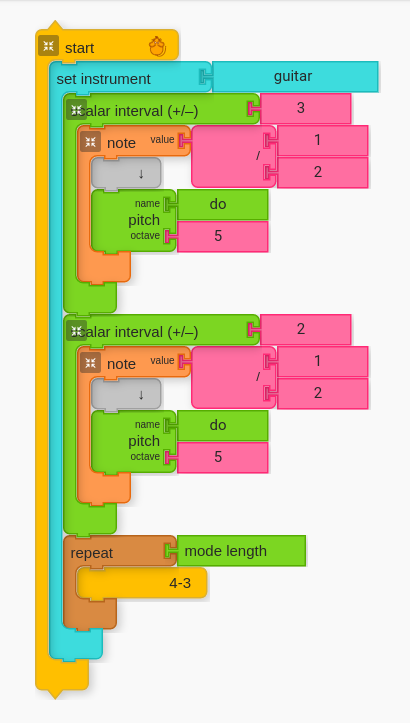
D. 2nd to 3rd

The following is moving from 2nd to 3rd (movement to the 3rd from below) with same structure as before.

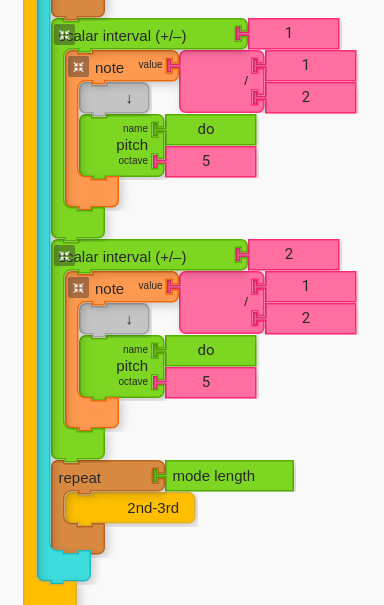
The structure to move from 2nd to 3rd is the same as 4th to 3rd motion. For 4th to 3rd, we are moving to the 3rd from above. For 2nd to 3rd, we are moving to the 3rd from below. In both cases we are starting from intervals of tension and moving into intervals of resolution.

G. All possibilities! (Advanced)

Below are all the possibilities. This may be a bit advanced for some groups of students, but it is nice to do if you have the time and a patient group of students. I had good success with the following with a middle school student, but I did not continue this far with a group of 3rd graders.

All possibilities ascending (going up)

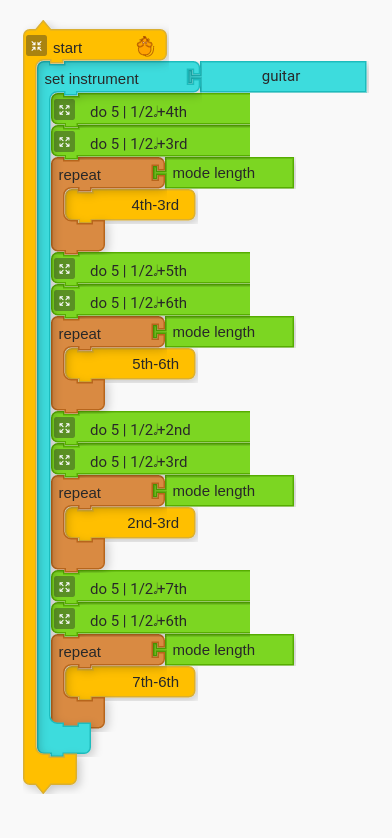
All ascending. By creating a script like the above, students can hear all possible motions into both 3rds and 6ths. As the play their code, ask them to actively listen to the quality of the sound. The goal is for the students to become sensitive to the different possibilities so that they can use them in their own compositions later.

Next, we can prepare to go both up and down by putting all of the ascending possibilities inside their own block.

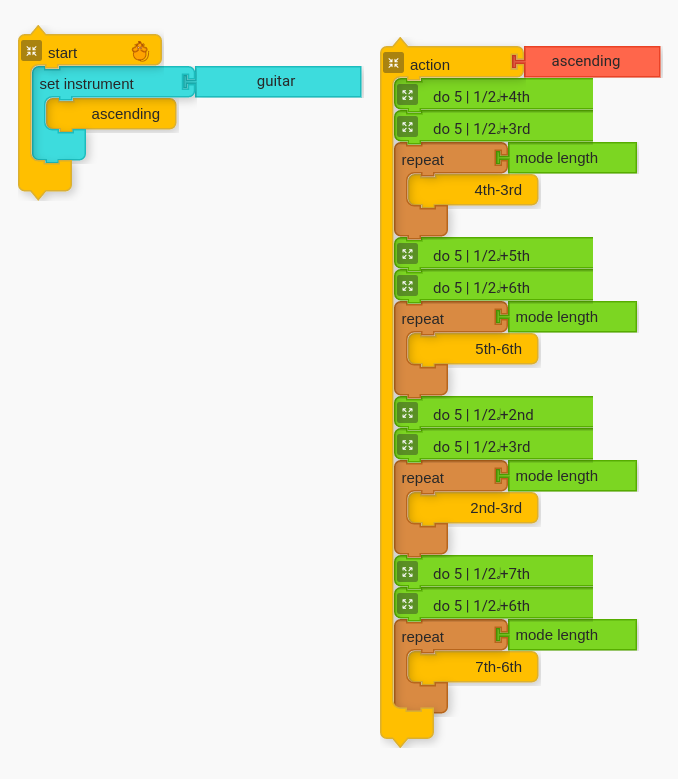
All possibilities descending (going down)

Once students have the formula for ascending, it is relatively simple to go down. The overarching structure is below.

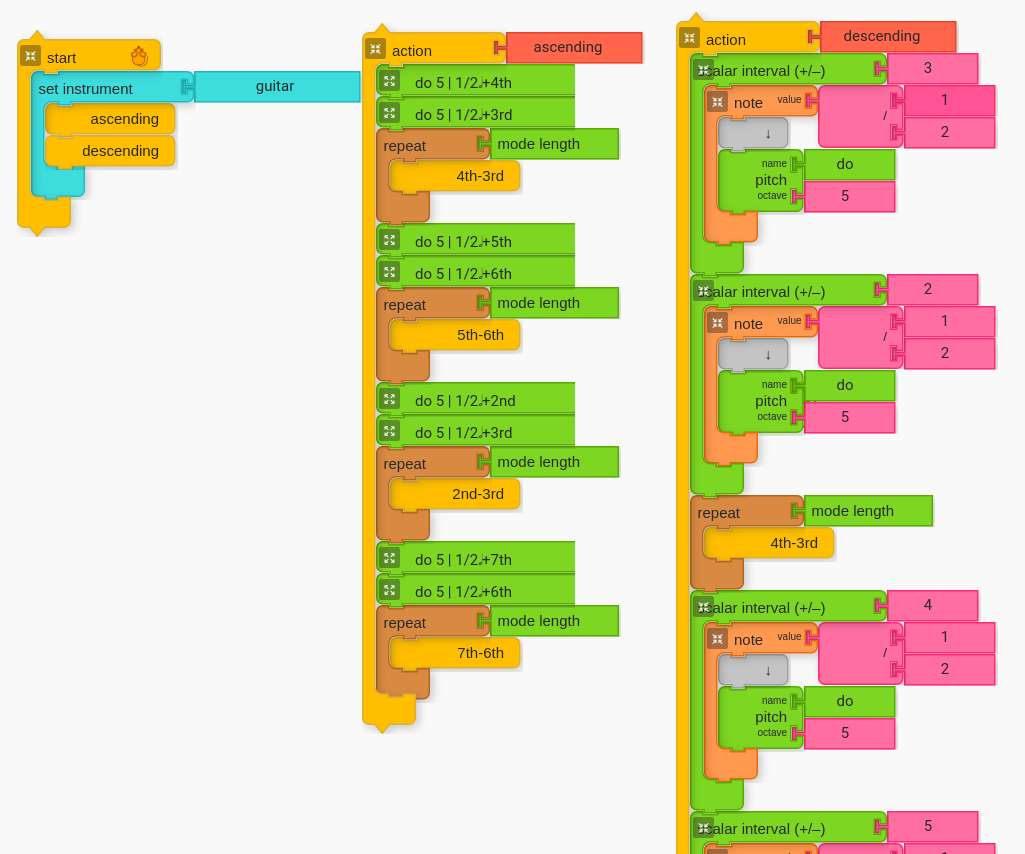
Students will need to copy their action blocks created for going up, and then modify them to go down. It is also important to rename the motion as well (e.g. “down” for all the ones going down and “up” for the ones going up).

Below is a step-by-step of the entire creation.

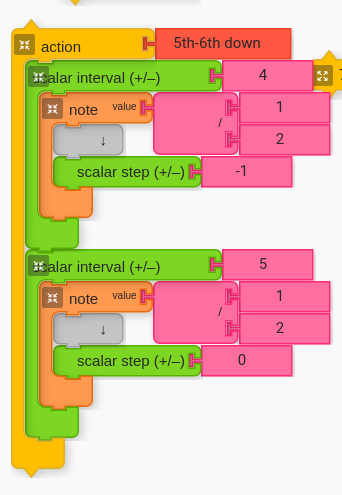
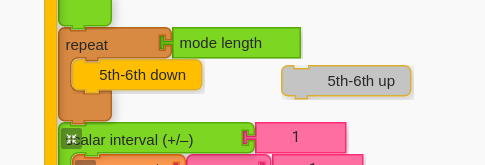
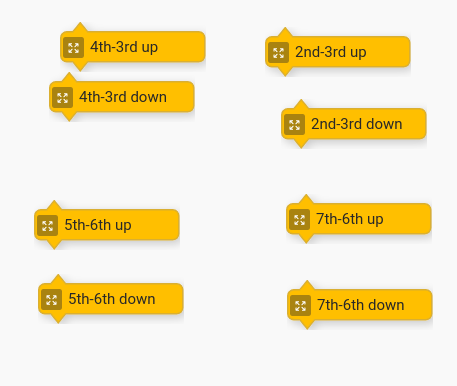
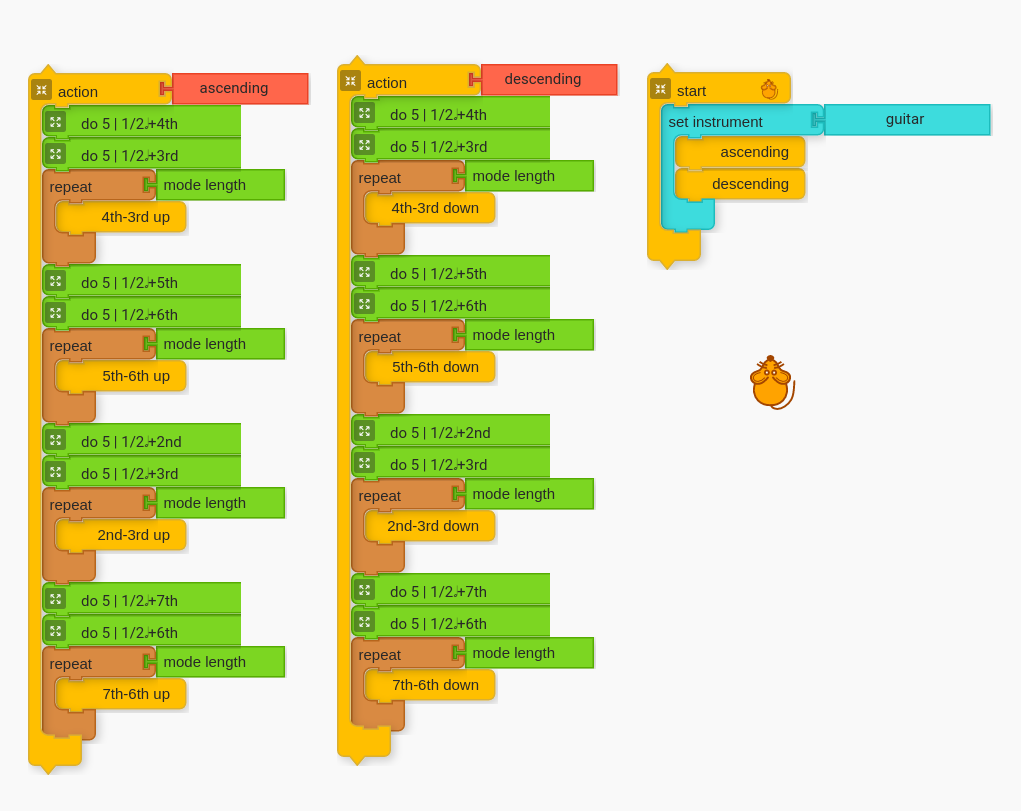
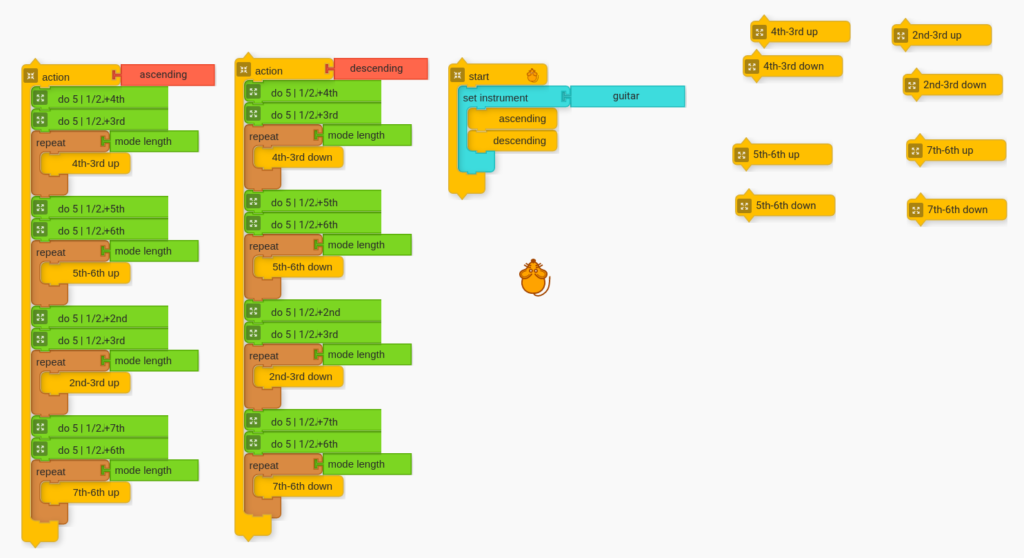
Once students have this script that runs through all the possibilities, ask students to find interval combinations that they like so that they may use them in their own compositions later. The goal is to get kids listening and making aesthetic decisions.

Performance/Critique

1. Have students showcase their creations for one another.
2. Have students share anything new they noticed about consonance and dissonance, tension and resolution, and thirds and sixths during the lesson.

Materials

• Paper and pencils for each student
• Music Blocks software (Computer, up-to-date browser)

Assessments

• Observe participation
• Do the students’ creations resolve to 3rds or 6ths (and of the same pitch as the tension)?
• Are students finding combinations that they like (so that they may use them for future compositions)?

Student/Teacher Projects

https://musicblocks.sugarlabs.org/index.html?id=1601479893965676&run=True is a teacher project that randomizes the melodic movement of the notes, but always has a 4-3 motion.

[[0,["start",{"id":1601732139302,"collapsed":false,"xcor":0,"ycor":0,"heading":0,"color":-10,"shade":60,"pensize":5,"grey":200}],259,195,[null,1,null]],[1,"settimbre",273,236,[0,2,13,3]],[2,["voicename",{"value":"flute"}],424,236,[1]],[3,"hidden",273,835,[1,null]],[4,["newnote",{"collapsed":false}],301,300,[13,5,8,12]],[5,"divide",403,300,[4,6,7]],[6,["number",{"value":1}],489,300,[5]],[7,["number",{"value":8}],489,332,[5]],[8,"vspace",315,332,[4,9]],[9,"pitch",315,364,[8,10,11,null]],[10,["solfege",{"value":"do"}],389,364,[9]],[11,["number",{"value":5}],389,396,[9]],[12,"hidden",301,458,[4,null]],[13,["interval",{"collapsed":false}],287,268,[1,14,4,15]],[14,["number",{"value":3}],472,268,[13]],[15,"hidden",287,489,[13,16]],[16,["interval",{"collapsed":false}],287,489,[15,17,18,27]],[17,["number",{"value":2}],472,489,[16]],[18,["newnote",{"collapsed":false}],301,521,[16,19,22,26]],[19,"divide",403,521,[18,20,21]],[20,["number",{"value":1}],489,521,[19]],[21,["number",{"value":8}],489,553,[19]],[22,"vspace",315,553,[18,23]],[23,"pitch",315,585,[22,24,25,null]],[24,["solfege",{"value":"do"}],389,585,[23]],[25,["number",{"value":5}],389,617,[23]],[26,"hidden",301,679,[18,null]],[27,"hidden",287,710,[16,53]],[28,["interval",{"collapsed":false}],684,227,[51,29,30,36]],[29,["number",{"value":3}],869,227,[28]],[30,["newnote",{"collapsed":false}],698,259,[28,31,34,35]],[31,"divide",800,259,[30,32,33]],[32,["number",{"value":1}],886,259,[31]],[33,["number",{"value":8}],886,291,[31]],[34,"vspace",712,291,[30,46]],[35,"hidden",698,417,[30,null]],[36,"hidden",684,448,[28,37]],[37,["interval",{"collapsed":false}],684,448,[36,38,39,45]],[38,["number",{"value":2}],869,448,[37]],[39,["newnote",{"collapsed":false}],698,480,[37,40,43,44]],[40,"divide",800,480,[39,41,42]],[41,["number",{"value":1}],886,480,[40]],[42,["number",{"value":8}],886,512,[40]],[43,"vspace",712,512,[39,47]],[44,"hidden",698,606,[39,null]],[45,"hidden",684,637,[37,null]],[46,"steppitch",712,323,[34,55,58]],[47,"steppitch",712,544,[43,48,null]],[48,["number",{"value":0}],848,544,[47]],[49,["action",{"collapsed":false}],670,186,[null,50,51,null]],[50,["text",{"value":"action"}],802,195,[49]],[51,"hidden",684,227,[49,28]],[52,["nameddo",{"value":"action"}],301,742,[53,null]],[53,"repeat",287,710,[27,54,52,null]],[54,["number",{"value":32}],389,710,[53]],[55,"random",848,323,[46,56,57]],[56,["number",{"value":-2}],939,323,[55]],[57,["number",{"value":3}],939,355,[55]],[58,"vspace",712,355,[46,null]]]